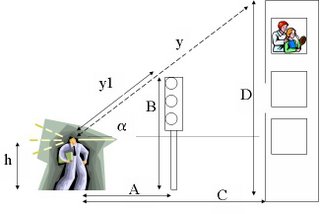
Algunos ejemplos de pensamiento fraccionario
Ésta es la clásica frontera aristotélica entre lo que se corrompe, lo mortal (lo que está debajo de la luna, el mundo terrestre) y lo eterno, lo divino (lo que está más allá de la luna, el mundo celeste: las estrellas fijas y los planetas). Esta fragmentación nos lleva a pensar que las propiedades y leyes de estos diferentes mundos son también diferentes. Aunque pudiera sostenerse que existía una influencia del mundo supralunar hacia el sublunar, esta influencia no se daba en sentido contrario por lo que ninguna relación podía extraerse que unificara el saber de un mundo con el otro.
Esta concepción será insuficiente cuando se estudien nuevos fenómenos gracias a instrumentos como el telescopio, que pondrá en evidencia que pueden existir explicaciones también basadas en la lógica que unificando los dos mundos en uno sean más satisfactorias (den cuenta de más fenómenos y de un modo más simple). La unificación más evidente se dará con la teoría de la gravitación universal de I. Newton.
Mundo Humano / Mundo Animal
Esta frontera separa lo que se suponen cualidades únicamente humanas del resto de la naturaleza. Es decir, tras observar el comportamiento y cualidades en nosotros mismos se llega a la conclusión de que todo aquello que no es nosotros mismos (el resto de seres vivos) no las tienen. Y no las tienen porque no son humanos y lo humano es aquello que -mediante ciertos criterios- sí vemos en los humanos. Aunque pueda parecer una tautología, es lógico llegar a esta manera de pensar, del mismo modo en como Aristóteles veía la corrupción de los cuerpos debajo de la luna pero nunca encima.
De nuevo, un estudio detallado de la naturaleza engrosa la lista de observaciones difíciles de explicar mediante esta simple fragmentación.
Otra manera de fraccionar más sutilmente la realidad es pensar que aún teniendo una evolución u origen común y aceptando que leyes iguales pueden regir a humanos y no humanos, el humano dispone de cualidades exclusivas que no se dan en ningún otro animal: la moralidad o la capacidad de simbolización. De nuevo, lo natural es pensar así, ya que la postura fraccionaria facilita u origina finalmente la empatía, y los principales destinatarios de esa empatía son el resto de individuos humanos. Lo lógico es ver ahí, en los propios individuos humanos, una persistente fragmentación con el resto de seres vivos.
así, ya que la postura fraccionaria facilita u origina finalmente la empatía, y los principales destinatarios de esa empatía son el resto de individuos humanos. Lo lógico es ver ahí, en los propios individuos humanos, una persistente fragmentación con el resto de seres vivos.
Las teorías que admiten las raíces de la moralidad en primates quedan replicadas con el argumento de que es nuestro prisma humano el que nos hace ver similitudes entre los animales y los humanos, pero que eso no implica que las haya. Contra el argumento de que todas las interpretaciones que podamos hacer de nuestro estudio de los animales están contaminadas de nuestra propia humanidad, poco puede decirse.
Ahora bien, si aceptamos como cierto ese argumento llegaremos a la conclusión de que el mero hecho de afirmarlo es producto de esa misma contaminación de nuestra humanidad, porque sino, ¿cómo estando permanentemente influenciados por nuestra visión de nosotros mismos podemos llegar a la conclusión de que estamos permanentemente influenciados por nuestra visión de nosotros mismos? El propio argumento, sin duda, es también resultado de nuestra imparcial mirada hacia el mundo y así ad infinitum. Este aparente callejón sin salida es insalvable desde la lógica aristotélica de la fragmentación porque utiliza una nueva lógica de carácter autoconsistente, en la cual aquellos elementos expuestos en el esquema de
Por un lado, mediante la lógica clásica fragmentamos la realidad; por el otro, mediante una lógica autoconsistente, argumentamos que esa fragmentación es insalvable. He ahí el quid de la cuestión y la solución al problema. En mi opinión, el origen de la fragmentación y su defensa argumentativa se apoyan en lógicas diferentes, lo cual -de algún modo- invalida las reglas del juego. Una analogía de esto sería:
Conclusión de
Si manejamos ambas conclusiones, vemos que en algún momento perdemos la capacidad de referirnos a B y a C, puesto que todo es A. Pero si todo es A, según
Se trata de una aparente desfragmentación sobre la fragmentación, diferente de lo que sería la vuelta a
Mundo partícula / Mundo No partícula
Lo natural es, de nuevo, reproducir nuestra visión cotidiana hacia lo que no percibimos cotidianamente. Y lo que no percibimos es lo más grande y lo más pequeño. Hacia lo más pequeño, los componentes últimos de todo lo que vemos aplicamos la fragmentación de pensar lógicamente eso: que hay componentes últimos, y que su suma o unión da cuentas de todo lo demás.
Así, llegamos al concepto de partícula (heredero del atomismo de Demócrito), confirmado incesantemente por las observaciones, tras las que asignamos propiedades y cualidades a unos componentes cuya razón de ser es en última instancia, arbitraria. Porque, ¿qué es aquello que no es partícula? El espaciotiempo es el marco conceptual en donde colocamos nuestra fragmentada realidad y a la vez, el marco y el contenido son en sí mismos el resultado de otra fragmentación.
Observaciones más detalladas –y aquí, más que observaciones son especulaciones matemáticas- nos hacen creer que una descripción más elaborada del espaciotiempo y de las partículas nos llevaría a unificar ambos conceptos, siendo estas últimas algo así como estados dimensionales especiales del espaciotiempo. De nuevo, parece que puede superarse la fragmentación! Pero surge, como siempre una nueva fragmentación: la que fragmenta el Todo en dimensiones. Una dimensión, otra dimensión, etc… hasta 10 ó más dimensiones en algunas teorías.
Como siempre, hemos pasado de una fragmentación a otra, aunque mucho más específica, más especulativa…
Y de nuevo, la pregunta: ¿es posible escapar de todas las fragmentaciones y obtener algún tipo de visión de

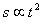






 Y Eureka! En la pared, a unos 5,51 m de distancia D de las rendijas, se pueden observar las interferencias claramente. La separación entre 2 máximos (entre el centro de la franja de luz central Po y el centro de la siguiente) es de 2,5 mm (de 2 a 3 mm). Veamos si concuerda con la teoría de Young.
Y Eureka! En la pared, a unos 5,51 m de distancia D de las rendijas, se pueden observar las interferencias claramente. La separación entre 2 máximos (entre el centro de la franja de luz central Po y el centro de la siguiente) es de 2,5 mm (de 2 a 3 mm). Veamos si concuerda con la teoría de Young.