¿Qué es derivar e integrar una función, y para qué sirve? (II. Integración)

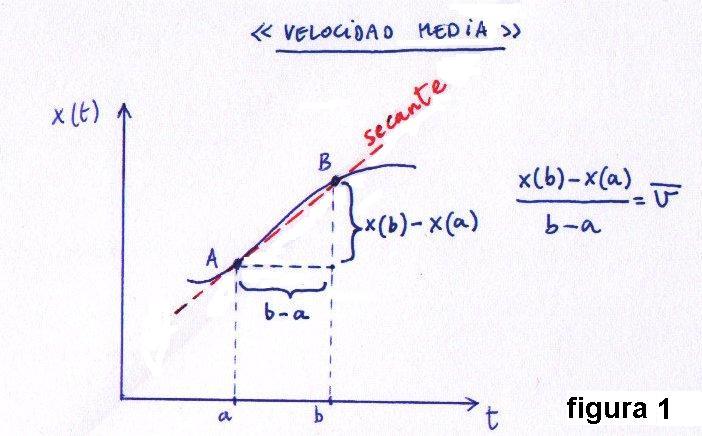
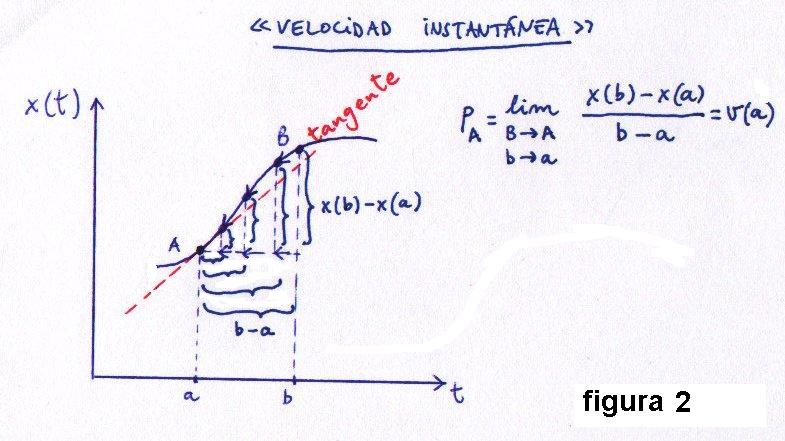
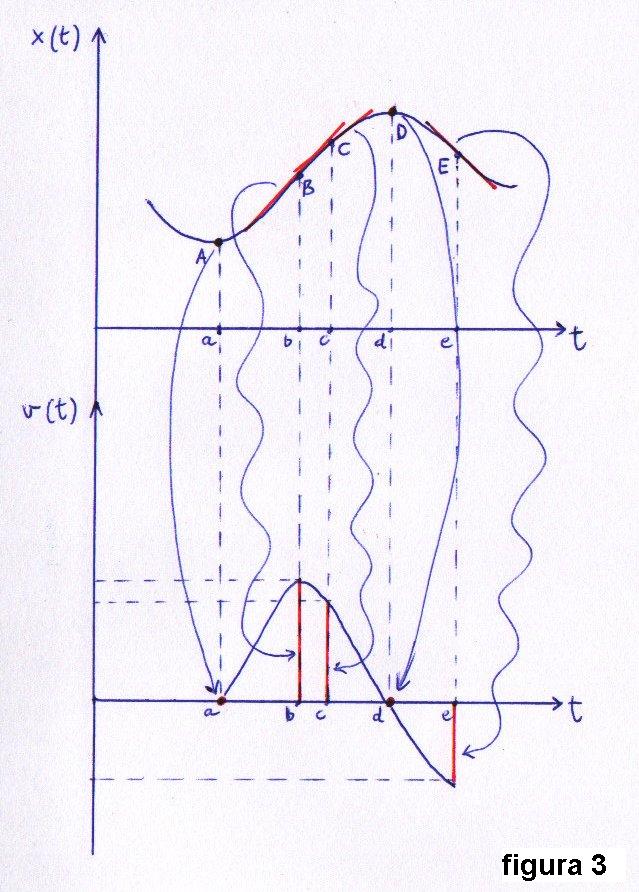
La Integral y el Teorema fundamental del cálculo

Hemos visto cómo hallando las pendientes de las tangentes de x(t) -ayudados por el concepto de límite- conseguimos obtener la fórmula de la velocidad v(t). A este método lo denominamos Derivación y a v(t) "la derivada de x(t)" (figura 3 del post anterior). Pero, ¿cuál es el paso inverso a la Derivación?, ¿cómo pasaríamos de la curva inferior v(t) a la superior x(t) en la figura 3?, ¿sabríamos reconstruir la posición a partir de la velocidad?

A este método inverso lo llamaremos "encontrar la Primitiva de v(t)".(Parece un buen nombre, ya que v(t) debe haberse generado originalmente a partir de x(t))

Tenemos las tangentes, pero no sabemos dónde colocarlas.

Probemos a reconstruir x(t) uniendo todas las tangentes una vez trasladadas desde v(t). Sabemos que las longitudes de los segmentos 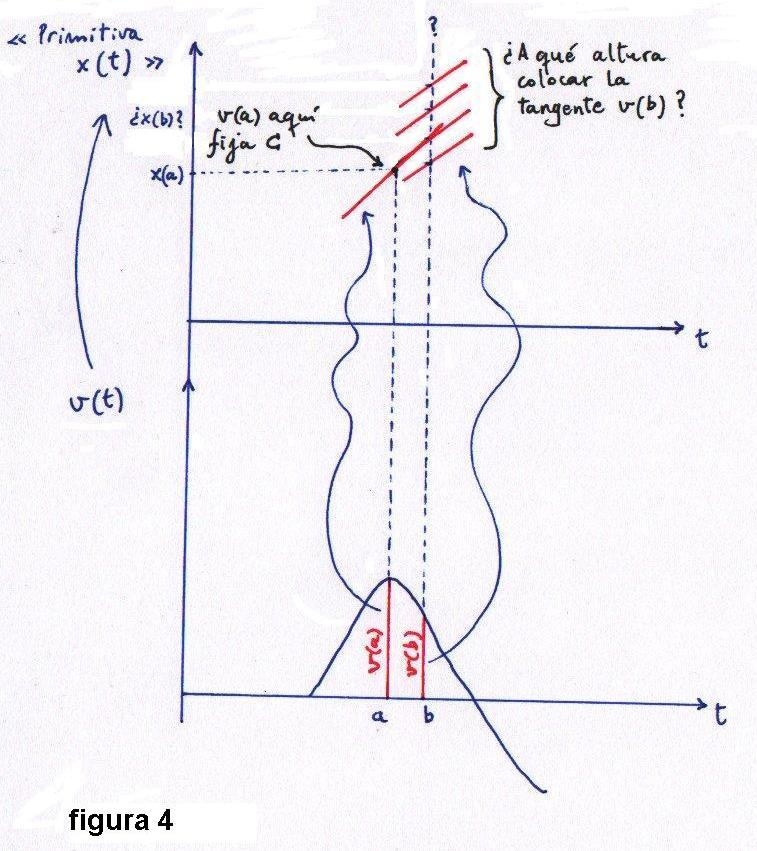rojos de v(t) -como el segmento v(a)- son justamente el valor de la pendiente de la tangente de una función x(t) cuando t=a. Para empezar, tomemos ese segmento y llevémoslo a la parte superior de la gráfica en la Figura 4. La inclinación será igual a la longitud del segmento, así que ya sabemos cómo inclinarlo... aunque no dónde ponerlo. Bueno, lo pondremos a la altura que queramos. Al fin y al cabo, ya vimos que infinitos corredores saliendo de diversas posiciones pueden describirse con la misma curva v(t) si corren de la misma forma. Al poner el segmento a una altura determinada estaremos fijando esa constante C de la que hablábamos en el post anterior. Ya tenemos x(a).
Ahora, procedamos igual con el segmento v(b) cuya longitud es menor, luego la pendiente o inclinación de la tangente en b de la curva primitiva será menor. Lo llevamos arriba con la inclinación correcta pero... ¡maldición! ¿Y ahora a qué altura lo debemos colocar respecto de x(a)? Necesitaríamos conocer la distancia vertical al punto conocido, es decir, la cantidad x(b) - x(a). Al tener C fijada, este paso no puede ser arbitrario. ¡Y sin ese dato no podremos reconstruir la curva primitiva x(t) que estamos buscando!

La integral: una suma muy especial.

Cabilemos un poco. Hemos tomado dos segmentos muy separados. Cuanto más juntos los tomemos, más iguales en altura los deberemos situar al trasladarlos arriba. Intuitivamente vemos que un ligero cambio en la curva primitiva x(t) en un pequeño intervalo de tiempo t debe corresponderse con un ligero cambio similar en v(t). Así, dos segmentos de v(t) muy juntos traladados deberían colocarse prácticamente a igual altura uno de otro en la construcción de x(t).
Por tanto, la información de cómo deben situarse las tangentes arriba -sus alturas relativas- debe estar de algún modo contenida en todos los segmentos de abajo muy muy próximos entre un intervalo dado. No podemos dejarnos ni un sólo segmento y deben trasladarse todos en bloque. Pero eso de muy muy próximos, en el límite, querrá decir "separados un intervalo infinitesimal dt", como definimos en el tema de la Derivación. Si están separados dt, conformarán una serie de rectángulos estrechísimos de base dt y altura (*) más o menos v(t), cuyas áreas sumadas nos darán el área total bajo la curva v(t) en ese intervalo. Al fin y al cabo, podemos concebir un área como una suma de líneas verticales muy pegadas, tal y como muchas hileras estrechamente enebradas conforman la superficie de un tapete.
Es a esta área total bajo la curva en un intervalo dado a lo que llamamos Integral. La Integral es una suma especial, de infinitas porciones infinitésimas. Por ello, tomamos la S de Suma y la estiramos por arriba y por abajo para hacer constar que es una suma muy muy larga: la S se convierte entonces en ese símbolo ∫ tan amado y odiado por muchos.
Pero, ¿qué información nos da la integral? Según nuestro razonamiento, debería decirnos dónde colocar los segmentos arriba, es decir, a qué alturas relativas deben estar todos para poder reconstruir nuestra primitiva x(t). Si abajo sumamos rectángulos infinitesimales entre a y b, arriba obtendremos la altura relativa entre x(b) y el x(a), porque eso es justamente la curva x(t): una diferencia de valores en un intervalo dado. De modo que, tomando intervalos [a,b] tan estrechos como queramos abajo, sabremos con exactitud cómo ir colocando todos los segmentos en la zona de x(t). Ver la figura 5.
Este es el llamado Teorema Fundamental del Cálculo, cuyo pomposo nombre es bien merecido, al menos por la increíble síntesis de conceptos que supone.

Abracadabra.

Veamos ahora porqué los seguidores de Leibniz describían su cálculo diferencial como cosa de magia. Otro modo de obtener este último resultado es aplicar que v(t)=dx/dt y cancelar los dt de numerador y denominador dentro de la integral. De este modo nos quedará el resultado metafísico de "suma de infinitésimas equis en el intervalo [a,b]", dibujado entre llaves rojas en la figura 6. Podemos interpretar esto como 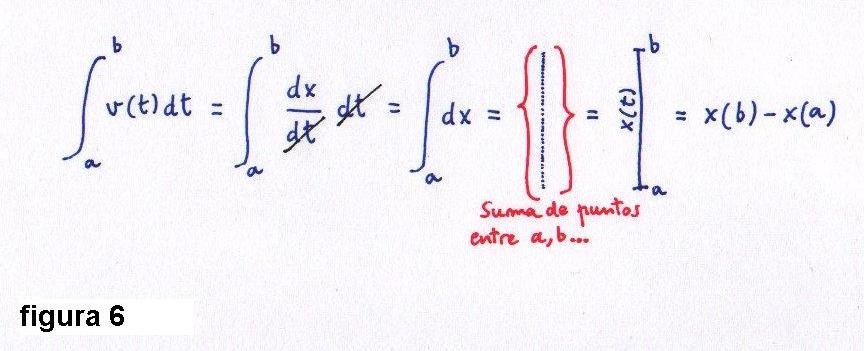una suma infinita de valores de equis tan próximos entre sí como queramos; y si sumamos puntos entre un intervalo dado lo que obtenemos es la longitud del propio intervalo, es decir, la diferencia de valores entre sus extremos: x(b) - x(a). ¡Tachán!



Un ejemplo del Teorema.

¿Cómo?, ¿aún no estáis sorprendidos? Entonces no me he explicado bien.
Veamos un ejemplo de la potencia de cálculo que todo esto supone: tomemos la curva de la velocidad del post anterior v(t)=2πt que habíamos obtenido derivando x(t). Pero cambiemos ahora la variable t por r. Ahora sí que nos resulta más familiar. Justamente, v(r)=2πr es la longitud de una circunferencia de radio r. Imaginemos que queremos conocer el área contenida dentro de una circunferencia de radio R. Es decir, queremos hallar la fórmula para el área de un círculo. Para ello, integramos v(r) en el intervalo de r=0 hasta r=R, y estaremos sumando infinitésimos rectángulos circulares de longitud circular 2πr y grueso dr. (Ver figura 7).
Bien, ¿cuánto vale esa integral ∫ v(r) dr de 0 a R?. Ni idea. Tal vez sea un cálculo muy complicado. Pero lo que sí sabemos es que la curva v(r) tiene como primitiva x(r)=πr² porque, dada la facilidad de hallar pendientes a una curva (mediante el concepto de límite), habíamos calculado anteriormente que 2πr era la Derivada de πr².
Así, que, por el Teorema Fundamental del Cálculo:

∫ v(r) dr = x(R) - x(0) = πR²

Ya tenemos el área del círculo!

Fijaos que no ha sido necesario tratar con series infinitas ni hacer interminables cálculos geométricos al estilo de los antiguos griegos... Acabamos de obtener una superficie basándonos sólo en el conocimiento de que la Derivada de πr² es 2πr.

Como hemos visto, el T. F. del Cálculo relaciona la Derivación (hallar pendientes de tangentes) con la Integración (sumar infinitas áreas infinitésimas). Y esto, de repente, se traduce en diferenciales que se cancelan por aquí y por allá y en tener bien a mano una serie de resultados de Derivación -más fáciles de calcular- para obtener primitivas de cualquier función. Bueno, pero no todo es tan bonito como parece, ya que podemos encontrar funciones que no puedan ser integradas por este método o toparnos al derivar con límites que no existan pero... ese ya es otro tema.
Por el momento, disfrutemos del éxito obtenido porque ésta es posiblemente la herramienta utilizada en el 99% de los problemas habituales de la ciencia moderna. Próximamente, veremos algunas disquisiciones más sobre ello. :-)

(Continuará)

(*): Esto de más o menos se hace evidente observando los rectángulos rojos de la figura 5. De hecho, al dividir en porciones cada vez más pequeñas la suma de todos se aproxima cada vez más al área total. Ésta es la llamada integral de Riemann. Sólo al final, la altura de cada rectángulo es realmente v(t). Que me perdonen los matemáticos... :-) Para ver el proceso con más rigor, véase por ejemplo esto.

¿Qué es derivar e integrar una función, y para qué sirve? (I. Derivación)

Todo lo que siempre quiso saber sobre Derivadas e Integrales y nunca se atrevió a preguntar...

Millones de personas las usan constantemente pero sólo unos pocos son conscientes de ello. Sin duda, la ciencia seguiría en pañales sin estas extraordinarias herramientas. Allá por el s. XVII, había dos problemas matemáticos cruciales: obtener las rectas tangentes a una curva y calcular áreas y volúmenes. Leibniz y Newton, independientemente, llegaron a comprender la profunda relación entre ellos... Comenzemos por un enfoque newtoniano de la derivación.

Las tangentes del movimiento

El estudio del movimiento de un cuerpo podía reducirse al estudio de su posición respecto del tiempo. En notación moderna, sería conocer la curva x(t). Y, como diría Newton, esta curva es una magnitud fluyente pues es el resultado de un punto que fluye contínuamente. Ahora bien, más allá de la posición, también querremos conocer la velocidad del cuerpo para estudiar la naturaleza dinámica de lo que está sucediendo (pues la velocidad nos dará información sobre la aceleración, que es la magnitud clave en la dinámica).
Para ello, podríamos calcular el cociente entre las diferencias de posición de dos puntos de la curva A y B y el tiempo entre ellos. Esto nos daría una velocidad, pero sería una velocidad media entre los dos puntos y no aportaría información sobre la velocidad instantánea en cada punto. Fijémonos en la figura 1, donde la recta que une ambos puntos es una secante a la curva. No sabríamos, por ejemplo, la velocidad real en A. Para conseguirlo, debemos calcular el cociente de esas mismas cantidades para diferencias muy pequeñas de tiempo, tomando dos puntos infinitamente próximos de modo que en el final de esa infinitud sean el mismo punto, en nuestro caso, el A. Así sabremos la velocidad instantánea v(a). Para Newton, esto se reducía a un cociente de dos cantidades que se desvanecen a la vez.
En la figura 2, vemos cómo el acercamiento de B hacia A implica esa disminución ad infinitum de las dos cantidades. Aquí, la recta final es una tangente a la curva en el punto A. En lenguaje moderno: obtenemos la pendiente PA haciendo el límite del cociente de ambas cantidades cuando B -> A ó lo que es igual, cuando b -> a. (Sólo es posible el límite si esa función cociente es continua, lo que no sería problema para Newton, ya que esta curva es el resultado de un punto que se mueve de forma continua, sin sobresaltos)

¡Y aquí entra en juego la famosa tangente! Fijémonos que ese cociente de dos cantidades que tienden a cero a la vez, al final, no es más que la pendiente de la recta tangente -en color rojo- a la curva en el punto A. De este modo, el valor obtenido será mayor cuánto más inclinada sea la recta tangente, cero si la tangente es horizontal (cuando A es un máximo o un mínimo en la curva la pendiente es nula) y positivo o negativo dependiendo de si la curva crece o decrece hacia la derecha.
Por tanto, el problema de hallar las tasas de cambio de una magnitud continua, como la de la posición respecto del tiempo (la velocidad) se reduce al arte de hallar tangentes a una curva. Lo haremos obteniendo la fórmula general para todas las tangentes de la curva posición usando el límite de la figura 2. A este proceso lo llamaremos Derivación o Diferenciación. Y a las cantidades x(b)-x(a) y b-a cuando b->a se las denominará diferenciales dx y dt respectivamente, indicando así que son cantidades infinitesimales o infinítamente pequeñas.

Jugando con las pendientes (de las tangentes)

Muy bien, ya sabemos calcular las velocidades instantáneas en cada posición de un cuerpo en movimiento. Dicho de otro modo, tenemos las tangentes. Representemos ahora esas rectas tangentes con una peculiaridad: serán segmentos de longitud igual al valor de la pendiente de la tangente. Observemos la parte superior de la figura 3 donde hemos dibujado en color rojo esos segmentos. En en el punto C, el segmento de la tangente tiene una determinada longitud, en B es de longitud mayor (mayor inclinación de la tangente, luego mayor pendiente) y en A y D es tan sólo un punto (ya que la pendiente de la recta tangente es nula).

Atención porque ahora viene lo bueno: tomemos esos segmentos y coloquémoslos en posición vertical en una nueva gráfica, en la parte inferior de la figura 3, construyendo una curva con ellos de modo que cada punto tenga como valor la altura del segmento. Si el segmento tenía un valor negativo de longitud como el del punto E (porque venía de una tangente con inclinación hacia abajo) lo colocaremos también hacia el sentido negativo del eje vertical. Unamos finalmente los puntos obtenidos mediante una curva e imaginemos que hemos procedido escrupulosamente para todos los puntos de la curva anterior, trasladando todas las tangentes. Lo que hemos hecho es Derivar la curva posición. Tenemos ahora una nueva curva que representa la velocidad en función del tiempo, ya que cada valor de la función es justamente la pendiente de las tangentes de la función posición anterior.
Observemos que, de haber dibujado la curva superior x(t) más arriba o más abajo en la gráfica, habríamos obtenido exactamente la misma curva v(t) de abajo, ya que ésta la hemos construido con las pendientes de las tangentes de x(t), y no se ve afectada por posibles desplazamientos verticales en x(t). Podemos entenderlo físicamente si imaginamos que varios corredores que comienzan una carrera desde diferentes posiciones (lo que equivale a sumar una constante a la función posición) tendrán la misma velocidad si corren de igual forma. Pero, mirando la figura 3, ¿qué misteriosa relación tiene esta curva inferior con la anterior?

Un caso imaginario de Derivación

Consideremos el caso imaginario en que la posición de un cuerpo varía con el tiempo según la extraña relación

x(t) = πt²

Es decir, en el instante t=1 segundo estará en la posición x= π metros, para t=2 segundos, en x= 4π metros y así sucesivamente.

Calculemos ahora la fórmula general para la pendiente de las rectas tangentes a la curva posición. Para ello, obtengamos primero la velocidad real en un instante t=a. Según lo visto en la figura 2, haremos:

v(a) = lim [(x(b)-x(a)) /(b-a)] = lim [(πb² - πa²) / (b-a)] = lim [π(b² - a²) / (b-a)] = lim π(b+a) = π(a+a) = 2πa
donde hemos usado que b² - a² = (b+a)(b-a) y donde lim se refiere al límite cuando b -> a

Vemos que en el caso general, para cualquier instante de tiempo t, tomando intervalos infinitesimales para hallar las tangentes,

v(t) = 2πt

Perfecto, ésta es la curva que describe cómo varía la velocidad del cuerpo cuya posición viene dada por πt². Diremos que la Derivada de πt² es 2πt. De hecho, en el caso general, si la curva posición tiene un desplazamiento vertical, -lo que equivale a sumarle una constante C- la curva v(t) será la misma, como hemos comentado en relación a la figura 3. Diremos entonces que las Derivadas de πt² + C son 2πt, para todas las ces. (Y C=0 es el caso particular que considerábamos)
Respecto a la notación, la más divulgada es la de Leibniz, donde dx/dt = v(t) o bien x'(t) = v(t) y en la notación más usada por Newton, x con un punto encima -cosa que no sé hacer con el teclado- significa también derivada respecto del tiempo, aunque él la llamaría fluxión de x. (Asímismo, al diferencial dt lo denota como o)
Bien, ya sabíamos que la derivada de la posición era la velocidad, pero ¿por qué es tan importante esta construcción de la función velocidad? ¿Y qué tiene que ver con el cálculo de áreas y volúmenes? Todo esto podría parecer un mero entretenimiento matemático si no fuera por las sorprendentes propiedades que encierra... pero, hagamos un breve descanso.

(Continuará)