La de que todos los cuerpos (graves) caen del mismo modo. Esto se traduce en su frase: los espacios recorridos en la caída [desde el reposo] son como los cuadrados de los tiempos.
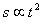
Nosotros diríamos que

siendo a la aceleración de la gravedad, unos 9,8 m/s², igual para todos los cuerpos.
Entonces, ¿la caída de un cuerpo no depende de su peso (nosotros diríamos, masa)? ¿No cae más rapido un cuerpo doblemente más pesado que otro? Es decir, observando nuestra fórmula, a es siempre la misma en un punto del espacio?
Veamos por un momento el legendario –por improbable- experimento de dejar caer dos cuerpos desde la torre de Pisa.
Consideremos dos cuerpos de masas m y m’= 2m dejados caer desde igual altura.
Durante su caída lo que va a ocurrir puede explicarse como si existiera una Fuerza de Gravitación (no olvidemos que son graves) que les atrae en dirección al centro de la Tierra (en la práctica cotidiana, hacia el suelo en línea recta). Esta fuerza puede describirse como

Ahora bien, toda fuerza aplicada sobre un cuerpo, sea la de Gravitación, eléctrica o de cualquier otro tipo, implica la aparición de una aceleración. Esta aceleración se ve contrarestada por la masa del cuerpo. De modo que, a igual Fuerza aplicada, cuanto mayor sea la masa, menor será la aceleración resultante, ya que su producto debe ser el mismo. Esta es la 2ª Ley de Newton.
Tras estas consideraciones, veámos cuál es la aceleración que se imprimirá en nuestros dos graves, dejados caer. En este caso, podemos igualar ambas fórmulas, ya que la única fuerza que actúa es la de Gravitación y debe cumplir también la 2ª Ley de Newton.
Así que, vemos que:

Las aceleraciones son iguales. Como el tiempo que tardarán en caer depende de la velocidad y ésta de la aceleración, ambos cuerpos caerán a la vez, independientemente de su masa. Ahora bien, lo que ocurre en la caída de los cuerpos no puede describirse sólo como si se vieran acelerados por una Fuerza Gravitatoria y desacelerados por una 2ª Ley de Newton. La caída acontece en un medio fluído, la atmósfera, que ofrece una resistencia adicional al paso del cuerpo. Esto se ve traducido en una fuerza en sentido contrario de la dirección de caída y que depende de la velocidad de caída, de la forma del cuerpo y de la densidad del aire. En ausencia de atmósfera, por tanto, todos los cuerpos caerían a la vez.
Observemos ahora las fórmulas (1) y (2). No hemos dudado en sustituir una en otra porque estábamos convencidos de que la Fuerza era la misma en ambas. Ahora bien, hemos procedido también de un modo totalmente gratuito pensando que ambas masas, la m de la fórmula (1) y la m de la fórmula (2) se refieren a la misma magnitud física. ¿Debería de serlo, a priori? El actuar así nos ha permitido obtener el resultado final, ya que hemos eliminado las masas de numerador y denominador como si fueran la misma. (De hecho, en nuestro ejemplo hemos simplificado el factor 2 arriba y abajo. Poder hacerlo implica que las masas m de arriba y abajo son la misma)
En verdad, podríamos llamar a la masa de (1) como gravitacional, ya que tiene que ver con la Fuerza de Gravitación, y a la masa de (2) como inercial, ya que actúa como una resistencia a acelerarse, es decir, se resiste a dejar su estado de inercia inicial.
Si admitimos nuestro resultado dando por buenas nuestra ley de caída de graves y nuestras leyes de inercia y Gravitatoria, llegaremos a la conclusión de que, si podemos actuar así, es porque
Masa gravitacional = Masa inercial Lo que más tarde, A. Einstein describiría como la intuición más maravillosa de mi vida, consistió en la visión de extrapolar este resultado al ámbito de los sistemas de referencia en su teoría de la Relatividad, entre otras consideraciones.
Lo que más tarde, A. Einstein describiría como la intuición más maravillosa de mi vida, consistió en la visión de extrapolar este resultado al ámbito de los sistemas de referencia en su teoría de la Relatividad, entre otras consideraciones.
